求斐波那契数列的通项（线代大作业）

交大版《线性代数》软件应用练习题10

斐波那契数列于1200年左右被发现，在现代物理、准晶体结构、化学等领域都有直接的应用，它把0和1作为初始项$F_0$和$F_1$，以后每一项作为前两项的和，$F_{k+2}=F_{k+1}+F_{k}$，于是得到数列1,1,2,3,5,83,1,21,$\cdots$. 求出斐波那契数列的通项.

既然作业要求是用MATLAB，那就先用一下。但是用计算机程序求通项公式好像不在我们的能力范围内，所以以下内容都是用程序求特定项，再用数学方法求出通项。

这个作业本来就很奇怪，真是让我不知道怎么理解才对。那就这么理解吧。

直接用库函数

注意到，MATLAB本身就提供了fibonacci函数，用来计算斐波那契数列的第n项。

clc 
clear all
X=sprintf("%d",fibonacci(114514));
disp(X);

那还写啥呢？

递推

无解析，因为没有什么必要。

MATLAB

function [Y]=f1bonacci(n)
X=0;
Y=1;
for i=2:n
    t=Y;
    Y=X+Y;
    X=t;
end
end

C++

long long fibonacci(int n)
{
    long long x=0,y=1,tmp;
    for(int i=2;i<=n;i++){
        tmp=y;y=x+y;x=tmp;
    }
    return y;
}

递归

同上

MATLAB

function [Y]=f1bonacci(n)
if(n==1||n==2)
    Y=1;
    return
else
    Y=f1bonacci(n-1)+f1bonacci(n-2);
    return
end
end

C++

long long fibonacci(int n)
{
    if(n==1||n==2) return 1;
    return fibonacci(n-1)+fibonacci(n-2);
}

运用矩阵

不喜欢运用矩阵。根本就是同样的东西，写成矩阵无非是更加装逼罢了。

It is my experience that proofs involving matrices can be shortened by 50% out

if one throws the matrices out.

—— Emil Artin

MATLAB

function [Y]=f1bonacci(n)
    M=[1,1;1,0];
    Init=[1;1];
    Res=(M^(n-2))*Init;
    Y=Res(1);
    return
end

运用高中数学

因为我比较笨（懒），不会用（懒得证）特征根法，所以就写一下等比数列的方法好了。

假设原递推式能变形为$a_{n}+A a_{n-1}=B\left(a_{n-1}+A a_{n-2}\right)$，记为$*$式

于是有$a_{n}=(B-A) a_{n-1}+A B a_{n-2}=a_{n-1}+a_{n-2}$

所以

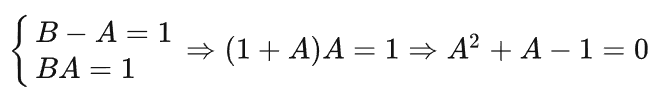
所以为什么fixit兼容性这么差 这个方程组只能帖图片了

后面的那些公式块也没法换行，太逊了。

解得

$$ A=\frac{-1 \pm \sqrt{5}}{2} $$ 再结合$*$式得 $$ \begin{aligned} a_{n}+A a_{n-1} & =B\left(a_{n-1}+A a_{n-2}\right) \ & =B^{2}\left(a_{n-2}+A a_{n-3}\right) \ & \cdots \ & =B^{n-2}\left(a_{n-(n-2)}+A a_{n-(n-1)}\right) \ & =B^{n-2}\left(a_{2}+A a_{1}\right) \ & =B^{n-2}(1+A) \ & =B^{n-1} \end{aligned} $$ 这样就得到了一个一阶线性递推式。

由于$a_{n}=-A a_{n-1}+B^{n-1}$

再次待定系数，假设$a_{n}+C B^{n}=-A\left(a_{n-1}+C B^{n-1}\right)$

由以上两式可得 $$ a_{n}=-A a_{n-1}-C A B^{n-1}-C B^{n}=-A a_{n-1}+B^{n-1} $$ 即 $$ -C A-C B=1 \Rightarrow C=\frac{-1}{A+B} $$ 代回原式得 $$ \begin{aligned} a_{n}+C B^{n} = & (-A)^{n-1}\left(a_{n-(n-1)}+C B^{n-(n-1)}\right) \ = & (-A)^{n-1}(1+C B) \ a_{n}= & (-A)^{n-1}(1+C B)-C B^{n} \ = & (-A)^{n-1}\left(1-\frac{B}{A+B}\right)+\frac{B^{n}}{A+B} \ = & \frac{(-A)^{n-1} A+B^{n}}{A+B} \ = & \frac{B^{n}-(-A)^{n}}{A+B} \end{aligned} $$ 此时再代入前面得到的A和B的值，即得最终的通项公式： $$ a_{n}=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\left(\frac{1-\sqrt{5}}{2}\right)^{n}\right] $$ 所以，在这个问题中，MATLAB到底能帮我什么呢？真是一个值得思考的问题。